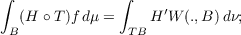|
One objective of this paper is to
prove a formula for the transformation of integrals by means of a change of
variable in purely measure—theoretic setting. The classical prototype of
such formulas is the one in which the change of variable is effected by an
(appropriately differentiable) one-to-one transformation from some subset of
Euclidean n-space Rn onto some other subset of Rn; the jacobian of the
transformation plays a key role here. For the present study the transformation which
gives the change of variable is no longer assumed to be one-to-one but it is
required to satisfy certain standard conditions relative to the measure spaces at
hand.
Some of the results presented in this paper can be summarized informally as
follows. Let T be a function from a nonempty set S onto a set X, let {S,M,μ} and
{X,N,ν} be measure spaces, and let B be a sub-σ-field of M. These entities are
subjected to certain standard requirements. Within this basic setting is proved a
formula which takes the form
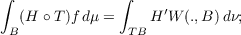 | (1) |
in (1), H is some N-measurable function, B is a set in B, f is analogous to the
jacobian, and ′W is a function having certain measure-theoretic properties. Indeed
′W(x,B) is intended to “count or weigh” the number of points in B mapped into x by
T. In this paper certain theorems are proved which reveal in detail the relationship
between f and ′W.
|