An embedding theorem for function spaces

Colin W. Clark

Vol. 19 (1966), No. 2, 243–251

DOI: 10.2140/pjm.1966.19.243

Abstract

Let G be an open set in E_n, and let H₀^m(G) denote the Sobolev space obtained by completing C₀^∞(G) in the norm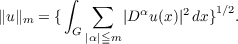

We show that the embedding maps H₀^m+1(G) ⊂ H₀^m(G) are completely continuous if G is “narrow at infinity” and satisfies an additional regularity condition. This generalizes the classical case of bounded sets G.

As an application, the resolvent operator R_λ, associated with a uniformly strongly elliptic differential operator A with zero boundary conditions is completely continuous in ℒ₂(G) provided G satisfies the same conditions. This generalizes a theorem of A. M. Molcanov.

Mathematical Subject Classification

Primary: 46.38

Milestones

Received: 12 May 1965

Published: 1 November 1966