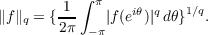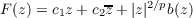Transformations of Fourier coefficients

Daniel Rider

Vol. 19 (1966), No. 2, 347–355

DOI: 10.2140/pjm.1966.19.347

Abstract

Let A and B be function spaces on the unit circle and let F be a complex function defined in the plane. F is said to map A into B provided ∑ F(a_n)e^in𝜃 is the Fourier series of a function in B whenever ∑ a_ne^in𝜃 is the Fourier series of a function in A. For 1 ≦ q < ∞, let L^q denote the usual space of functions on the unit circle normed by

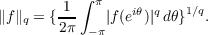(1)

Let 2 ≦ q ≦∞ and p be given by p⁻¹ + q⁻¹ = 1.

It follows from the Hausdorff-Young theorem that if b(z) is bounded near the origin, then

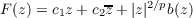(2)

maps L^q into L^q.

In this paper it is shown that all functions mapping L^q into L^q have this form. In fact, all functions mapping the continuous functions into L^q have this form.

Theorem 1. Let 2 ≦ q ≦∞. The following are equivalent.

(i) F maps L^q into L^q.

(ii) F maps the continuous functions into L^q.

(iii) F(z) = c₁z + c₂z + |z|^2∕pb(z) where b(z) is bounded near the origin.

Mathematical Subject Classification

Primary: 42.10

Milestones

Received: 7 June 1965

Published: 1 November 1966