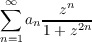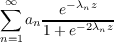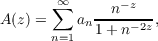The exponential analogue of a generalized Weierstrass series

George Joseph Kertz and Francis Regan

Vol. 19 (1966), No. 3, 461–466

DOI: 10.2140/pjm.1966.19.461

Abstract

The generalized Weierstrass series

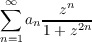
has as its exponential analogue

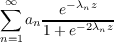
where {a_n} is a sequence of complex-valued constants and {λ_n} is any real-valued strictly monotone increasing unbounded sequence.

In this paper the λ_n will be chosen to be ln n. Then the above series becomes

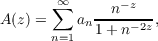(1)

hereafter called simply the A-series. In its region of absolute convergence an A-series can be expressed as a Dirichlet series; conversely, a Dirichlet series can be represented by an A-series. Under restrictions on the sequence {a_n}, the imaginary axis becomes a natural boundary of the function represented by the A-series.

Mathematical Subject Classification

Primary: 30.24

Milestones

Received: 4 October 1965

Published: 1 December 1966