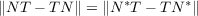On operators whose spectrum lies on a circle or a line

Herbert Meyer Kamowitz

Vol. 20 (1967), No. 1, 65–68

DOI: 10.2140/pjm.1967.20.65

Abstract

The purpose of this note is to prove the following theorem. THEOREM. Let N be a bounded linear operator on Hilbert space H satisfying

(1)

for all bounded linear operators T. Then N is (obviously) normal and the spectrum of N lies on a circle or straight line.

Here N^∗ denotes the adjoint of the operator N.

It is clear that if S is a unitary or self-adjoint operator and α and β are complex numbers, then N = αI + βS satisfies (1). The theorem asserts that the converse is also true.

Mathematical Subject Classification

Primary: 47.40

Milestones

Received: 27 April 1965

Published: 1 January 1967