|
Throughout this paper G
denotes a locally compact group and {Hn} denotes an increasing sequence of closed
subgroups of G whose union H is dense in G. For each n,Δn denotes the
modular function on Hn and Δ denotes the modular function on G. Then
limnΔn(x) = Δ(x) for each x ∈ H. For each n,λn denotes a left Haar measure on
Hn and λ denotes a left Haar measure on G. For a function f on G and an x in
G,xf denotes the function xf(y) = f(xy). The main theorem states that if
Δn is the restriction of Δ to Hn for all sufficiently large n, then there is a
“normalizing” sequence {αn} of positive numbers such that for every f in
L1(G,λ)
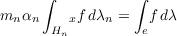 | (1) |
for λ-locally almost all x in G. The hypotheses regarding the Δn’s and Δ hold in all
cases known to the authors. In particular, they hold if the Hn’s are unimodular
(hence if they are Abelian, compact, or discrete) or if the Hn’s are open subgroups or
normal subgroups. If G is the compact group  0,1 0,1 with addition modulo 1, if the
Hn’s are the finite groups {k2−n : 0 ≦ k ≦ 2n − 1} with counting measure λn, and if
αn = 2−n, then the left side of (1) is a Riemann sum and (1) becomes Jessen’s
theorem. with addition modulo 1, if the
Hn’s are the finite groups {k2−n : 0 ≦ k ≦ 2n − 1} with counting measure λn, and if
αn = 2−n, then the left side of (1) is a Riemann sum and (1) becomes Jessen’s
theorem.
|





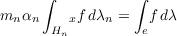

 with addition modulo 1, if the
with addition modulo 1, if the
