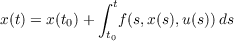|
Let f = (f1,f2,⋯,fn) be a
mapping to En from a set D in E1 × En × Em; and f0 a real function on D.
Consider a “control” function u from an interval I = [t0,t1] in E1 to En; and a
“response” function x from I to En such that (t,x(t),u(t)) ∈ D for almost every
t ∈ I,f0(t,x(t),u(t)) has an integral (finite or +∞) on I,f(t,x(t),u(t)) is integrable
on I, and
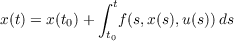 | (1) |
for all t ∈ I. In a class Γ of such control-response pairs (u,x), a pair (u∗,x∗) is called
optimal (with respect to f0) if the “cost” functional

has a minimum at (u∗,αj∗). Here we consider conditions sufficient for existence of
such optimal pairs.
|