|
|||||

|

|
|

|

|
|
On the convergence of
quasi-Hermite-Fejér interpolation
K. K. Mathur and R. B. Saxena |
|
Vol. 20 (1967), No. 2, 245–259
|
Abstract |
|
The present paper deals with the convergence of quasiHermite-Fejér interpolation series {Sn(x,f)} satisfying the conditions 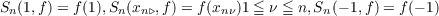 and 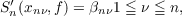 where βnν’s are arbitrary numbers; xn0 = 1,xnn+1 = −1 and {xnν} are
the zeros of orthogonal polynomial system {pn(x)} belonging to the weight
function (1 − x2)p|x|q,0 < p ≦ |
Mathematical Subject Classification
Primary: 41.10
|
Milestones
Received: 12 September 1962
Revised: 12 May 1964
Published: 1 February 1967
|
Authors |
| K. K. Mathur | |
| R. B. Saxena | |
 |
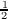 ,
, 