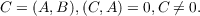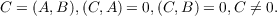|
Let K be a field of
characteristic p,p zero or prime, and let L be the algebraic closure of K. Let Mn(K)
denote the matrix algebra of n-square matrices with elements in K. The commutator
of A,B ∈ Mn(K) is defined by (A,B) = AB − BA. It is the object of this paper to
examine the following two questions.
I. Given exactly one of the three matrices A,B,C ∈ Mn(K), to determine
necessary and sufficient conditions in order that the other two matrices will exist in
Mn(K) such that
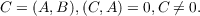 | (1) |
II. Given exactly one of the three matrices A,B,C ∈ Mn(K), to determine
necessary and sufficient conditions in order that the other two matrices will exist in
Mn(K) such that
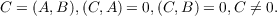 | (2) |
We shall obtain complete solutions to all these problems, except that, in Question
I when C is the given matrix and 0 < p ≦ n, we obtain only a partial solution. As a
consequence of our results, we are able to find conditions that are sufficient, and
sometimes necessary and sufficient, in order that solutions exist in Mn(K)
for certain complicated families of commutator equations related to (1) or
(2).
|