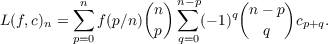|
The purpose of this
paper is to pair classes of continuous functions from [0,1] to the complex
numbers with classes of complex sequences. If f is a function from [0,1] to
the complex numbers and c is a complex sequence, a sequence L(f,c) is
defined:
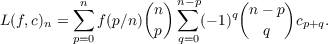
A class A of continuous functions is paired with a class B of sequences provided
that
(1) if f is in A and c is in B then L(f,c) converges,
(2) if f is a continuous function and L(f,c) converges for each c in B then f is in
A, and
(3) if c is a sequence and L(f,c) converges for each f in A then c is in
B.
We establish the following pairings:
CONTINUOUS | SEQUENCES |
|
| all continuous functions | Hausdorff moment sequences |
|
| power-series absolutely
convergent at 1 | bounded sequences |
|
| power-series absolutely
convergent at r(r < 1) | sequences dominated
by geometric sequences having
ratio r |
|
| entire functions | all sequences dominated by
geometric sequences |
|
| polynomials | all sequences |
|
| | |
|