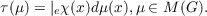|
Let G be a locally compact
idempotent, commutative, topological semigroup (semi-lattice). Let ℳ(G) denote its
measure algebra, i.e., ℳ(G) consists of all countably additive regular Borel-measures
defined on G and has the usual Banach algebra structure: pointwise linear operations,
convolution, and total variation norm. To understand the structure of such a
convolution algebra one studies its maximal ideals, the nature of the Gelfand
transform, the structure of the closed ideal and the related question of spectral
synthesis, etc.
In this paper G is the carlesian product of topological semigroups Gα of the
following form: Gα is a linearly ordered set, locally compact in ils order topology;
multiplication in Gα is given by xy = max(x,y). The product semigroup is assumed
locally compact in the product topology.
The main theorem of this paper gives a representation of the space of maximal
ideals Δℳ(G), for a finite product, in terms of the dual semigroup Ĝ. The
multiplicative linear functionals of ℳ(G) are integrals of fixed semi-characters
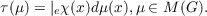
It is shown that this integral representation does not hold for infinite products
because the semi-characters are usually not integrable.
|