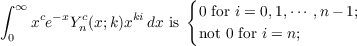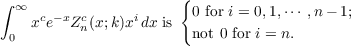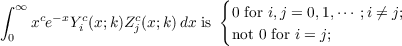Biorthogonal polynomials suggested by the Laguerre polynomials

Let Y _n^c(x;k) and Z_n^c(x;k),n = 0,1,⋯ , be polynomials of degree n in x and x^k, respectively, where x is real, k is a positive integer and c > −1, such that

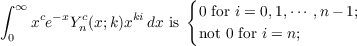{ ∫ ∞ c −x c ki 0 for i = 0,1,⋅⋅⋅ ,n − 1; x e Yn(x;k)x dx is not 0 for i = n; 0

(1)

and

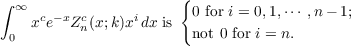∫ ∞ { xce−xZcn(x;k)xidx is 0 for i = 0,1,⋅⋅⋅ ,n− 1; 0 not 0 for i = n.

(2)

For k = 1, conditions (1) and (2) reduce to the orthogonality requirement satisfied by the generalized Laguerre polynomials.

If (1) and (2) hold, then

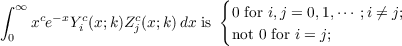
∫ { ∞ c −x c c 0 for i,j = 0,1,⋅⋅⋅ ;i ⁄= j; 0 x e Yi (x;k)Zj(x;k)dx is not 0 for i = j;

and conversely.

For both sets of polynomials, we shall establish mixed recurrence relations from which we shall derive differential equations of order k + 1. From these mixed recurrence relations pure recurrence relations connecting k + 2 successive polynomials can also be obtained. For k = 1, the recurrence relations and the differential equations for both of the polynomial sets reduce to those for the generalized Laguerre polynomials.

Mathematical Subject Classification

Primary: 33.40

Milestones

Received: 9 September 1965

Published: 1 May 1967

Authors

Joseph D. E. Konhauser

Vol. 21, No. 2, 1967

Joseph D. E. Konhauser

Abstract

Mathematical Subject Classification

Milestones

Authors