A transplantation theorem for Jacobi coefficients

Richard Allen Askey

Vol. 21 (1967), No. 3, 393–404

DOI: 10.2140/pjm.1967.21.393

Abstract

Let f(𝜃) be integrable on (0,π) and define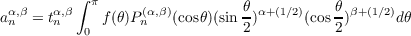

where P_n^(α,β)(x) is the Jacobi polynomial of degree n, order (α,β) and

Then if α,β,γ,δ ≧−1∕2 we have

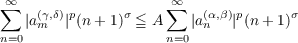for 1 < p < ∞,−1 < σ < p − 1 whenever the right hand side is finite.

From this result any norm inequality for Fourier coefficients can be transplanted to give a corresponding norm inequality for Fourier-Jacobi coefficients.

Mathematical Subject Classification

Primary: 42.15

Secondary: 33.00

Milestones

Received: 1 April 1966

Published: 1 June 1967