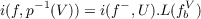|
Let ℱ = (E,p,B) be a
(Hurewicz) fibre space and let λ be a lifting function for ℱ For W a subset of B, a
map f : p−1(W) → E is called a fibre map if p(e) = p(e′) implies p(f(e)) = p(f(e′)).
Define f : W → B to be the map such that f−p = pf. If [W ∪ f(W)]−⊆ V ⊆ B
where V is pathwise connected, define fbV : p−1(b) → p−1(b), for b ∈ W, by
fbV (e) = λ(f(e),ω)(1) where ω;I → V is a path such that ω(0) = f(b)− and
ω(1) = b. Let i be a fixed point index defined on the category of compact ANR’s and
let Q denote the rationals. The main result of this paper is: THEOREM 1.
Let ℱ = (E,p,B) be a fibre space such that E,B, and all the fibres are
compact ANR’s. Let f : E → E be a fibre map. If U is an open subset of B
such that f(b)≠b for all b ∈ bd(U) and cl [U ∪ f−(U)] ⊆ V ⊆Ḃ where V is
open and pathwise connected and ℱ|V = (p−1(V ),p,V ) is Q-orientable,
then
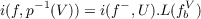
where L(fbV ) is the Lefschelz number of fbV for any b ∈ U.
|