|
|||||

|

|
|

|

|
|
Properties of
differential forms in n real
variables
Henry B. Mann, Josephine Mitchell and Lowell Schoenfeld |
|
Vol. 21 (1967), No. 3, 525–529
|
Abstract |
|
We prove the following theorem. Let ℒX be a homogeneous elliptic operator of the second order with constant coefficients. Let f be a Lebesgue integrable solution of ![ℒX [f(X )] = 0](a140x.png) for all X in some neighborhood of the point A in the Euclidean space En. Let X = (x1,⋯,xn) and H = (h1,⋯,hn). Then for each p = 1,2,⋯ the homogeneous polynomial φp(H;f) defined by 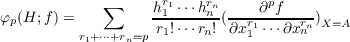 is an indefinite form, or is identically zero, and it satisfies the same differential equation ℒH[φp(H;f)] = 0 for all H ∈ En. Analogous differential relations are true for the solutions of homogeneous hypoelliptic equations of any order. The infinite differentiability of these solutions is called upon. |
Mathematical Subject Classification
Primary: 35.42
|
Milestones
Received: 30 December 1965
Published: 1 June 1967
|
Authors |
| Henry B. Mann | |
| Josephine Mitchell | |
| Lowell Schoenfeld | |
 |
