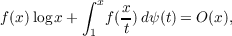|
The elementary proofs of
the prime number theorem are essentially based on asymptotic equations of the
form
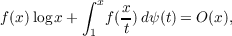 | (A) |
where f(x) is some function concerning the primes, ψ(x) is Tchebychev’6 function
and the limits in the integral—as throughout in this paper—are taken from 1—to
x+. This paper gives an elementary method for refining the right hand side of
(A).
This method is based on the lemma of Tatuzawa and Iseki [2], and, assuming the
prime number theorem, on an estimation of remainder integral which is more
accurate than earlier ones.
|