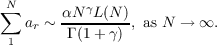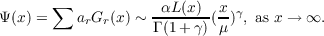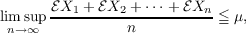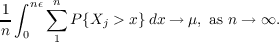|
{Xn} is a sequence of
independent, nonnegative, random variables and Gn(x) = P{X1 + ⋯ + Xn ≦ x}.{an}
is a sequence of nonnegative constants such that, for some α > 0,γ > 0, and function
of slow growth L(x),
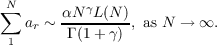
A Generalized Elementary Renewal Theorem (GERT) gives conditions such that, for
some μ > 0,
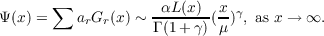 | (*) |
The Weak Low of Large Numbers (WLLN) states that (X1 + ⋯ + Xn)∕n → μ, as
n →∞, in probability. Theorem 1 proves that WLLN implies (*). Theorem 3 proves
that (*) implies WLLN if, additionally, it is given that (i) ∑
1nP{Xj > n𝜖}→ 0 as
n →∞, for every small 𝜖 > 0; (ii) for some 𝜖 > 0,n−1 ∑
1n ∫
0n𝜖P{Xj > x}dx is a
bounded function of n. Theorem 2 supposes the {Xn} to have finite expectations and
proves (*) implies WLLN if it is given that
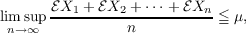
in which case (ℰX1 + ⋯ + ℰXn)∕n necessarily tends to μ as n →∞. Finally, an
example shows that (∗) can hold while the WLLN fails to hold. Much use is made of
the fact that a necessary and sufficient condition for the WLLN is that, for all small
𝜖 > 0,
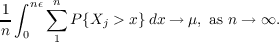
|