Tensor products of group algebras

Bernard Russel Gelbaum

Vol. 22 (1967), No. 2, 241–250

DOI: 10.2140/pjm.1967.22.241

Abstract

Let G,H,K be Iocally compact abelian groups where K is noncompact and both the quotient G∕N^e where N^e is a compact (normal) subgroup and the quotient H∕N^1T where N^E is a compact (normal) subgroup. Then in a natural fashion the group algebras L₁(G) and L₁(H) are modules over L₁(K) and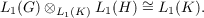

Mathematical Subject Classification

Primary: 42.56

Secondary: 46.00

Milestones

Received: 20 July 1966

Published: 1 August 1967