Estimates for the transfinite diameter with applications to confomral mapping

Melvyn Klein

Vol. 22 (1967), No. 2, 267–279

DOI: 10.2140/pjm.1967.22.267

Abstract

Let f(z) be a member of the family S of functions regular and univalent in the open unit disk whose Taylor expansion is of the form: f(z) = z + a₂z² + ⋯ . Let D_w be the image of the unit disk under the mapping: w = f(z). An inequality for the transfinite diameter of n compact sets in the plane {T_i}₁ⁿ is established, generalizing a result of Renngli: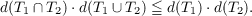

This inequality is applied to derive covering theorems for D_w relative to a class of curves issuing from w = 0, arcs on the circle: |w| = R as well as other point sets.

Mathematical Subject Classification

Primary: 30.41

Milestones

Received: 22 August 1966

Published: 1 August 1967