Ergodic properties of nonnegative matrices. I

David Vere-Jones

Vol. 22 (1967), No. 2, 361–386

DOI: 10.2140/pjm.1967.22.361

Abstract

This paper contains an attempt to develop for discrete semigroups of infinite order matrices with nonnegative elements a simple theory analogous to the Perron-Frobenius theory of finite matrices. It is assumed throughout that the matrix is irreducible, but some consideration is given to the periodic case. The main topics considered are

(i) nonnegative solutions to the inequalities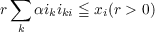

(ii) nonnegative solutions to the inequalities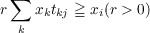

(iii) the limiting behaviour of sums P_j(n;r) = ∑ _ku_kt_kj⁽ⁿ⁾rⁿ. as n →∞, where {u_k} is arbitrary nonnegative vector. An extensive use is made of generating function techniques.

Mathematical Subject Classification

Primary: 60.65

Secondary: 15.00

Milestones

Received: 4 October 1965

Revised: 26 October 1966

Published: 1 August 1967