On some hyponormal operators

V. Istrăţescu

Vol. 22 (1967), No. 3, 413–417

DOI: 10.2140/pjm.1967.22.413

Abstract

Let H be a Hilbert space and T a hyponormal operator (T^∗T − TT^∗≧ 0). The first result is: if (T^∗)^pT^q is a completely continuous operator then T is normal.

Secondly, part we introduce the class of operators on a Banach space which satisfy the condition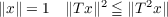

and we prove the following:

1. γ_T = lim∥Tⁿ∥^1∕n = ∥T∥;

2. if T is defined on Hilbert space and is completely continuous then T is normal.

Mathematical Subject Classification

Primary: 47.10

Milestones

Received: 22 December 1965

Published: 1 September 1967