On constructing distribution functions: A bounded denumerable spectrum with n limit points

Daniel Paul Maki

Vol. 22 (1967), No. 3, 431–452

DOI: 10.2140/pjm.1967.22.431

Abstract

If {a_n}₀^∞ and {b_n}₁^∞ are real sequences with the b_n’s all positive, then a theorem of Favard states that there exists a bounded increasing function ψ(x) which is a distribution function for the polynomial set {ϕ_n}₋₁^∞ which is recursively defined as follows: ϕ₋₁(x) ≡ 0,ϕ₀(x) ≡ 1,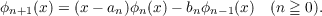

This study considers the problem of constructing ψ(x) for certain classes of sequences {a_n}₀^∞ and {b_n}₁^∞. The sequences considered all lead to functions ψ(x) which have a bounded denumerable spectrum with n limit points (1 ≦ n < ∞).

Mathematical Subject Classification

Primary: 42.15

Milestones

Received: 14 July 1966

Published: 1 September 1967