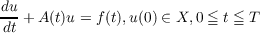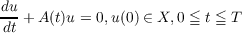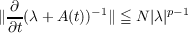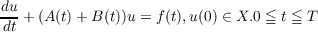|
In this paper, the regularity of
the solution of the initial value problem for the abstract evolution equation
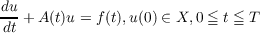 | (0.1) |
and the associated homogeneous equation
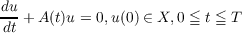 | (0.2) |
in a Banach space X is considered. Here u = u(t) and f(t) are functions from [0,T]
to X and A(t) is a function on [0,T] to the set of (in general) unbounded linear
operators acting in X.
Definition. u(t) is called a strict solution of (0.1) or (0.2) in (s,T] if
(i) u(t) is strongly continuous in the closed interval [s,T] and is strongly
continuously differentiable in the semiclosed interval (s,T],
(ii) u(t) ∈ D(A(t)), the domain of A(t), for each t ∈ (s,T],
(iii) u(t) satisfies (0.1) resp. (0.2) in (s,T],u(s) coinciding with the given initial
value at t = s. It is assumed that A(t) for each t ∈ [0,T] satisfies the following
conditions.
(i) −A(t) generates a semigroup exp(−sA(t)) of operators analytic in the sector
|arg s| < 𝜃,s≠0,0 < 𝜃 < π∕2,
(ii) For any complex number λ satisfying |arg λ| < π∕2 + 𝜃,
0 < 𝜃 < π∕2,(∂∕∂t)(λ + A(t))−1 exists in the operator topology and that there
exist constants N and ρ independent of t and λ with N > 0,0 ≦ ρ < 1 such
that
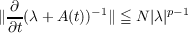
The main result proved in the paper can be stated as follows. If, in addition to the
above assumptions, A(t)−1 ∈ Cn+α[0,T] in the uniform operator topology,
B(t), a bounded operator for each t ∈ [0,T] is of class Cn−1+β[0,T], and
f(t) ∈ Cn−1+γ[0,T] in the strong topology, then the unique strict solution u(t)
of
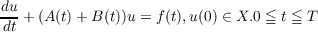
belongs to the class Cn+δ[s0,T],s0 > 0 arbitrary, δ > 0 depending on α,β,γ and ρ.
In this no assumption regarding the constancy of the domain D(A(t)) is
made.
|