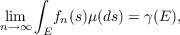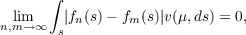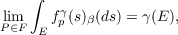|
Suppose that Σ is a field of
subsets of the set S, and suppose that μ and γ are complex-valued finitely additive
set functions defined on Σ. Assume that μ is bounded and γ is finite and
absolutely continuous with respect to μ. (A word of warning is in order here. The
statement γ is absolutely continuous with respect to μ” is often interpreted as
“μ(E) = 0 implies γ(E) = 0”. This is not the meaning used here. Our definition is
“for every 𝜖 > 0 there is a δ > 0 such that |β(E)| < δ implies |γ(E)| < 𝜖.”
Unless μ is bounded and countably additive, the two definitions are not
equivalent.)
THEOREM 1. There exists a sequence {fn} of μ-simple functions on S, such
that
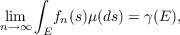 | (1) |
uniformly for E ∈ Σ
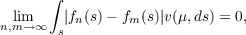 | (2) |
where v(μ) is the total variation of μ.
Theorem 1 is established by a pure existence proof, and gives no indication of how
to find fn. A more constructive result is given below.
A partition of S is a finite collection of sets Ei belonging to Σ, such that S is the
disjoint union of the Ei, and such that μ(Ei)≠0,i = 1,⋯,n.
The set 𝒫 of partitions may be directed by refinement, that is, by the following
partial order: P1 < P2 if for every E ∈ P1 there exist F1,⋯,Fr ∈ P2 ( r may depend
on E) such that E and ⋃
i=1rFi differ by a μ-null set.
If P is a partition of S, define the μ-simple function fpγ to be ∑
E∈P(γ(E)∕μ(E))χE,
where χE is the characteristic function of E.
THEOREM 2. If ∕ℓ is positive, then
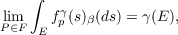
uniformly for E ∈ Σ, where 𝒫 is directed as explained above.
|