Addition theorems for sets of integers

Calvin T. Long

Vol. 23 (1967), No. 1, 107–112

DOI: 10.2140/pjm.1967.23.107

Abstract

Let C be a set of integers. Two subsets A and B of C are said to be complementing subsets of C in case every c ∈ C is uniquely represented in the sum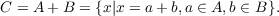

In this paper we characterize all pairs A,B of complementing subsets of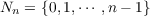

for every positive integer n and show some interesting connections between these pairs and pairs of complementing subsets of the set N of all nonnegative integers and the set I of all integers. We also show that the number C(n) of complementing subsets of N_n is the same as the number of ordered nontrivial factorizations of n and that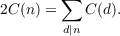

Mathematical Subject Classification

Primary: 10.62

Milestones

Received: 15 February 1966

Revised: 22 August 1966

Published: 1 October 1967