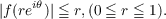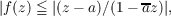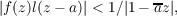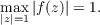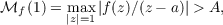|
If f(z) is an analytic
function, regular in |z|≦ 1,|f(z)|≦ 1 for |z| = 1 and f(O) = 0, then by Schwarz’s
lemma
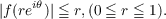
More generally, if f(z) is regular inside and on the unit circle, |f(z)|≦ 1 on the
circle and f(a) = 0, where |a| < 1, then
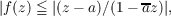 | (1) |
inside the circle. In other words,
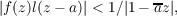 | (2) |
for |z|≦ 1. For a fixed a on the unit circle, let Ca denote the class of functions f(z)
which are regular in |z|≦ 1, vanish at the point z = a, and for which
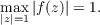
Any positive number A being given, it is clearly possible to construct a function f(z)
of the class Ca for which
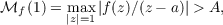
i.e. ℳf(1) is not uniformly bounded for f ∈ Ca. If f(z) is restricted to a subclass of
Ca there may exist a uniform bound for ℳf(1) as f(z) varies within the subclass. It
is clear that such is the case for the important subclass consisting of all polynomials
of degree at most n vanishing at z = a. The problem is to find the uniform
bound.
|