Hilbert transforms for the p-adic and p-series fields

Keith Lowell Phillips

Vol. 23 (1967), No. 2, 329–347

DOI: 10.2140/pjm.1967.23.329

Abstract

In this paper, a class of singular integral transforms of the Calderón-Zygmund type is constructed for the spaces L_r(Ψ_p,λ);Ψ_p is the p-adic or p-series field, λ is additive Haar measure, 7^⋅ > 1. The transforms have the form

where m is the modular function for the field and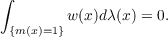

The fundamental result is the existence of the L_r-limit and the NI. Riesz inequality ∥Lf∥_r ≤ A_r∥f∥_r. Several examples of functions w defining transforms L are given. In particular, subsets Φ of Ψ_p such that Φ ∩−Φ = ∅ and Φ ∪−Φ = Ψ_p∖{0} together with functions w satisfying w(−x) = −w(x) yield transforms which are analogues of the classical Hilbert transform. Multipliers for L are also discussed. A preliminary theorem of independent interest states that the L₂-Fourier transform on certain 0-dimensional locally compact Abelian groups converges pointwise.

Mathematical Subject Classification

Primary: 47.70

Secondary: 42.00

Milestones

Received: 23 June 1965

Revised: 8 August 1966

Published: 1 November 1967