Measures whose range is a ball

Neil William Rickert

Vol. 23 (1967), No. 2, 361–371

DOI: 10.2140/pjm.1967.23.361

Abstract

It has been shown by R. P. Kaufman and the author that if μ is a measure of total variation 1 with values in Rⁿ, then there is a measurable set E with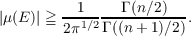

The main purpose of this paper is to determine for which measures μ there is no set E with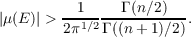

It will be shown that they are the measures which satisfy the following two conditions:

(i) The measure of the whole space is zero.

(ii) The induced probability measure α ∘ f(|μ|) on the projective space Pⁿ⁻¹ is orthogonally invariant, where f = dμ∕d|μ| maps the measure space to the sphere Sⁿ⁻¹ and α is the natural map of Sⁿ⁻¹ onto Pⁿ⁻¹.

Mathematical Subject Classification

Primary: 28.50

Milestones

Received: 22 August 1966

Revised: 3 May 1967

Published: 1 November 1967