A characterization of restrictions of Fourier-Stieltjes transforms

Haskell Paul Rosenthal

Vol. 23 (1967), No. 2, 403–418

DOI: 10.2140/pjm.1967.23.403

Abstract

The main result that we prove here is as follows: Let E be a Lebesgue measurable subset of R, the real line, and let φ be a bounded measurable function defined on E. Then the first of the following conditions implies the second: (1) There exists a constant K, so that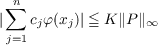

for all trigonometric polynomials of the form P(y) = ∑ _j=1ⁿc_je^ix_jy, where x_j ∈ E for all 1 ≦ j ≦ n. (2) φ is E-almost everywhere a Stieltjes transform. Precisely, there exists a finite (complex Borel) measure μ, so that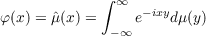

for almost all x ∈ E. Moreover, μ may be chosen such that ∥μ∥≦ K, where K is the constant in (1). (∥μ∥ denotes the total variation of μ.)

Mathematical Subject Classification

Primary: 42.25

Milestones

Received: 17 January 1967

Published: 1 November 1967