|
|||||

|

|
|

|

|
|
Integral equivalence of
vectors over local modular lattices
John Sollion Hsia |
|
Vol. 23 (1967), No. 3, 527–542
|
Abstract |
|
Let F be a local field with characteristic unequal to two, and in which the element 2 is not unitary. Let V be a regular quadratic space over F,L a lattice on V . The group of units of L is the subgroup 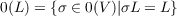 of the orthogonal group 0(V ). Two vectors u and v in L are defined to be integrally equivalent if there exists an isometry σ ∈ 0(L) mapping one onto the other. This paper gives necessary and sufficient conditions for integral equivalence of vectors when the underlying lattice L is modular. |
Mathematical Subject Classification
Primary: 15.70
|
Milestones
Received: 31 January 1967
Revised: 2 April 1967
Published: 1 December 1967
|
Authors |
| John Sollion Hsia | |
 |
