Convolution operators on L^p(G) and properties of locally compact groups

John Eric Gilbert

Vol. 24 (1968), No. 2, 257–268

DOI: 10.2140/pjm.1968.24.257

Abstract

A locally compact group G is said to have property (R) if every continuous positive-definite function on G can be approximated uniformly on compact sets by functions of the form s ∗s,s ∈𝒦(G). When μ is a bounded, regular, Borel measure on G, the convolution operator T_μ defined by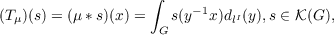

can be extended to a bounded operator on L^p(G) whose norm satisfies ∥T_μ∥_p ≦∥μ∥. In this paper three characterizations of property (R) are given in terms of the norm ∥T_μ∥_p, 1 < p < ∞, for specific operators T_μ. From these characterizations some closely-related, but seemingly weaker properties than (R), are shown to be equivalent to (R). Examples illustrating the results are given also.

Mathematical Subject Classification

Primary: 22.65

Milestones

Received: 31 January 1967

Published: 1 February 1968