|
In general the exact solution
of the differential system
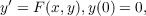
is either unattainable or is impractical to handle, even though a solution is known to
exist and may even be obtained in certain cases. Thus some method of approximation
is often employed. After the choice of approximating functions has been made, there
still remains the questions of goodness of approximation and, if infinite processes are
employed, the question of convergence.
The system described above is restricted in this paper to those cases in which
F(x,y) is an analytic function of x and y for −1 ≦ x ≦ 1 and all y. Then F(x,y) can
be written as a convergent power series
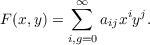
By considering a sequence of n-th degree polynomials {Pnk(x)} which are
𝜖-approximate solutions of the truncated system
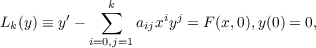
the solution of the original system can be uniformly approximated by polynomials
which satisfy Pnk(0) = 0 and which minimize
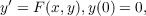
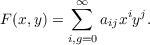
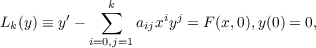
![k k
∥F(x,0)− Lk[Pn(x)]∥ = s0≦uxp≦1 |F (x,0)− Lk [Pn (x)]|.](a103x.png)
|
