A stability theorem for a third order nonlinear differential equation

J. L. Nelson

Vol. 24 (1968), No. 2, 341–344

DOI: 10.2140/pjm.1968.24.341

Abstract

A stability theorem and a corollary are proved for a nonlinear nonautonomous third order differential equation. A remark shows that the results do not hold for the linear case. THEOREM. Let p′(t) and q(t) be continuous and q(t) ≧ 0, p(t) < 0 with p′(t) ≧ 0. For any A and B suppose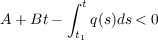

for large t where Q(t) = ∫ _t0^tq(s)ds, then any nonoscillatory solution ixj(t) of the equation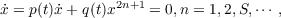

has the following properties; sgn x = sgn X,≠ sgn ẋ,lim_t→∞ẍ(t)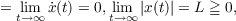

and x(t)X(t),X(t) are monotone functions. COROLLARY. If q(t) >∈> 0 for large t, then lim_t→∞x(t) = 0.

Mathematical Subject Classification

Primary: 34.50

Milestones

Received: 1 February 1967

Published: 1 February 1968