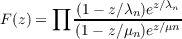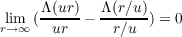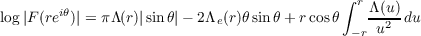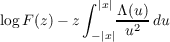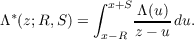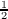|
Throughout this paper {λn} is
a real sequence with λn≠0 and λn ≦ λn+1,−∞ < n < ∞. The counting function
Λ1(u) is the number of λn between 0 and u, counted negatively for negative u.
Similarly μn is a real sequence with μn≠0 and with counting function Λ2(u).
In this summary (which corresponds to the case p = 1 of the paper) we
define
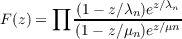
by taking all factors for which λn and ∕xn lie on the interval (−R,R) and then
letting R →∞. Our objective is to obtain conditions on the growth of F(z) from
conditions on the function Λ(u) = Λ1(u) − Λ2(u).
Denoting the even part of Λ(u) by Λe(u), we can state our first result as follows:
Suppose Λ(u) = O(u) and
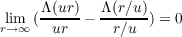
for each u≠0. Then
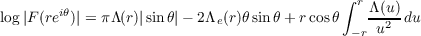
apart from an error term ηr log |2csc𝜃|, where η → 0 uniformly in 0 < |𝜃| < π as
r →∞. This improves theorems of Pfluger, Kahane and Rubel, Cartwright, and
others, in that we do not assume existence of limΛ(u)∕u, we do not assume that F is
entire or even, and the error term has a convergent integral with respect to 𝜃.
Similar theorems for functions with negative poles and zeros, given later in
the paper, generalize other familiar results. Here the error term involves
log(2sec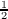 𝜃). 𝜃).
Another kind of result is briefly described as follows: Let R = R(x) and S = S(x)
be positive functions such that the ratios x∕R,R∕x,x∕S,S∕x are bounded as
|x|→∞. Then for many purposes the function
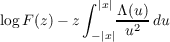
can be replaced by the function
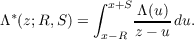
This remark is given content by detailed estimates of the error and of Λ∗. (For
simplicity of statement the text takes R = S but the form mentioned here is
sometimes more convenient, and is allowed by the proofs.) The development leads to
a simple, systematic method of proving variety of growth theorems. Formulation of
such a method is a principal goal of this paper, and our specific examples are
intended only for illustration.
|