A representation of a bounded function as infinite product in a domain with Bergman-Shilov boundary surface

Maciej Skwarczyński

Vol. 25 (1968), No. 1, 177–183

DOI: 10.2140/pjm.1968.25.177

Abstract

In this paper we consider a closed domain Q in the space of two complex variables along with its decomposition into two parameter family q(λ₁,λ₂) of segments of analytic surfaces. Under some additional assumptions about the domain Q one introduces using Poisson formula the real-valued functions of the real extended class. These functions are harmonic in each q(λ₁,λ₂). This in turn enables us to define the complex valued functions of the complex extended class. The aim of the paper is to show that a bounded analytic function which has infinitely many zero surfaces n_s(z) = 0, z = (z₁,z₂), s = 1,2,⋯ can be represented in the domain Q in the form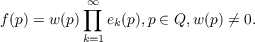

Here e_k(p) are functions of the complex extended class.

Mathematical Subject Classification

Primary: 32.02

Milestones

Received: 23 March 1967

Published: 1 April 1968