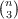|
Generalizing the conccpt of the
triangular association scheme, Bose and Laskar introduced the tetrahedral graph the
vertices of which are the 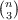 unordered triplets selected from n symbols with two
points adjacent if and only if their corresponding triplets have two symbols in
common. If we let d(x,y) denote the distance between two vertices x, y and Δ(x,y)
the number of vertices adjacent to both x and y, then the tetrahedral graph possesses
the following 4 properties: unordered triplets selected from n symbols with two
points adjacent if and only if their corresponding triplets have two symbols in
common. If we let d(x,y) denote the distance between two vertices x, y and Δ(x,y)
the number of vertices adjacent to both x and y, then the tetrahedral graph possesses
the following 4 properties:
(B0) the number of vertices is 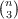
(B1) it is connected and regular of degree 3(n − 3)
(B2) if d(x,y) = 1 then Δ(x,y) = n − 2
(B3) if d(x,y) = 2 then Δ(x,y) = 4.
The question whether these conditions characterize tetrahedral graphs (no loops
or parallel edges permitted) was answered in the affirmative by Bose and Laskar for
n > 16. In the present paper characterizations of tetrahedral graphs are derived by
strengthening each one of (B1), (B2), (B3) and these results are utilized to prove the
sufficiency of (B0)–(B3) for n = 6. (For n < 4 the problem is void, n = 4,5 are trivial
cases.)
|





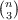 unordered triplets selected from
unordered triplets selected from