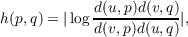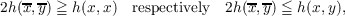|
The interior of a closed convex
curve C in the Euclidean plane can be given a Hilbert metric, which is preserved by
projective mappings. Let p, q be points interior to C and let u, v be the points of
intersection of the line pq with C. The Hilbert distance h(p,q) is defined
by
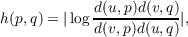
where d(x,y) denotes Euclidean distance. If C contains at most one line segment
then h(p,q) is a proper metric and the metric lines are the open chords of C carried
by the Euclidean lines. Following Busemann [1, p. 237], we define the (qualitative)
curvature at a point p as positive or negative if there exists a neighborhood U of p
such that for every x,y ∈ U we have
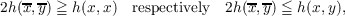
where x y are the Hilbert midpoints of p and x and of p and y respectively.
In an earlier paper [2] we proved that any point p at which the sign
of the curvature is determined is a projective center of C; that is, there
exists a projective transformation which maps p into an affine center of the
image of C. We also stated the conjecture that a Hilbert geometry has no
point of positive curvature. It is the purpose of this paper to prove that
conjecture.
|