Theorems on Brewer sums

Stanley F. Robinson

Vol. 25 (1968), No. 3, 587–596

DOI: 10.2140/pjm.1968.25.587

Abstract

Let V _m(x,Q) be the polynomial determined by the recurrence relation

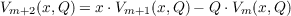(1)

(m = 1,2,⋯), Q an integer, with V ₁(x,Q) = x and V ₂(x,Q) = x² − 2Q. In a recent paper, B. W. Brewer has defined the sum

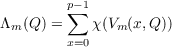(2)

where χ(s) denotes the Legendre symbol (s∕p) with p and odd prime.

The purpose of this paper is to consider the evaluation of Λ_2n(Q) when n is odd. The principle result obtained is the expression of Λ_2n(Q) as the sum of χ(Q) ⋅ Λ_n(1) and one half the character sum ψ_2e(1). ψ_2e(1) can in turn be expressed in terms of the Gaussian cyclotomic numbers (i,j). The values of Λ₆(Q) and Λ₁₀(Q) follow immediately from this result utilizing values for Λ₃(1) = Λ₃ and Λ₅(1) = Λ₅ computed by B. W. Brewer and A. L. Whiteman.

Mathematical Subject Classification

Primary: 10.41

Milestones

Received: 8 August 1966

Revised: 1 November 1967

Published: 1 June 1968