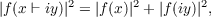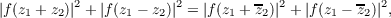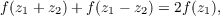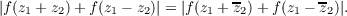|
Several authors have solved
the Pythagorean functional equation
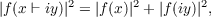 | (1) |
where f is an entire function and x and y are real variables.
A simple computation shows that, if f is a solution of (1), then f is also a
solution of
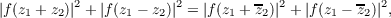 | (2) |
where z1 and z2 are complex variables. (If an entire function vanishes at the origin
and is a solution of (2), then it is a solution of (1), and conversely.) If an entire
function f is a solution of Jensen’s functional equation
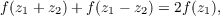 | (3) |
where z1 and z2 are complex variables, then it is also a solution of
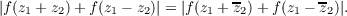 | (4) |
In this paper we shall prove that a solution of (4) is always a solution of (2). Then
we shall solve certain functional inequalities derived from (2) and use the solutions to
solve (1), (2), (3), and (4).
|