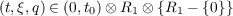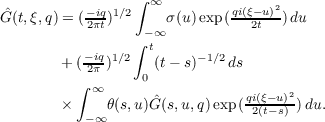Generalized Ilstow and Feynman integrals

Let C[a,b] denote the space of continuous functions x(t) defined on [a,b] ∋ x(a) = 0. This space is called Wiener space. Using the Wiener integral we define, for each nonnegative integer M, what we call the M Ilstow, M complex Wiener, M Feynman, limiting M complex Wiener, and limiting M Feynman integrals of a functional F(x) on C[a,b] and show various relationships which exist between these integrals. In particular we give necessary and sufficient conditions for a finite dimensional functional F(x) to be M Ilstow integrable on C[a,b].

We consider the set of linear functionals x(t₁),⋯,x(t_n) where a = t₀ < t₁ < ⋯ < t_n = b and obtain conditions on g_j(u) ∋ the functional

F(x) = g1[x(t1)]⋅⋅⋅gn[x(tn)]

(1.1)

is M Ilstow and limiting M Feynman integrable on C[a,b]. We then apply these results to the functional

∫ b F(t,ξ,x ) = exp( 𝜃[t− s,x(s)+ ξ]ds)σ[x(t)+ ξ] a

where 0 ≦ t ≦ t₀, −∞ < ξ < ∞ and x ∈ C[0,t₀] and show that for appropriate functions 𝜃(t,ξ) and σ(ξ), the limiting M Feynman integral Ĝ(t,ξ,q) of F(t,ξ,x) exists for

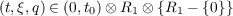
(t,ξ,q) ∈ (0,t0)⊗ R1 ⊗ {R1 − {0}}

and satisfies there the integral equation

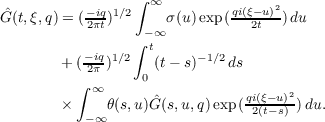∫ ˆ −iq 1∕2 ∞ qi(ξ−u)2 G (t,ξ,q) = (2πt) − ∞σ(u)exp( 2t )du ∫ t + (−2iπq)1∕2 (t − s)−1∕2ds ∫ ∞ 0 × 𝜃(s,u)Gˆ(s,u,q)exp(qi(ξ−u)2) du. −∞ 2(t−s)

(1.2)

Mathematical Subject Classification

Primary: 28.46

Milestones

Received: 28 April 1967

Published: 1 July 1968

Authors

David Lee Skoug

Vol. 26, No. 1, 1968

David Lee Skoug

Abstract

Mathematical Subject Classification

Milestones

Authors