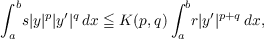|
In this paper certain
inequalities involving integrals of powers of a function and of its derivative are
proved. The prototype of such inequalities is Opial’s Inequality which states that
2∫
0X|yy′|dx ≦ X ∫
0Xy′2 dx whenever y is absolutely continuous on [0,X] with
y(0) = 0. The extensions dealt with here are all integral inequalities of the
form
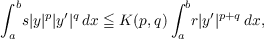
(or with ≦ replaced by ≧), where r, s are nonnegative, measurable functions on
I = [a,b], and y is absolutely continuous on I with either y(a) = 0, or y(b) = 0, or
both. In some cases y may be complex-valued, while in other cases y′ must not
change sign on I. The inequality (as stated) is obtained in case pq > 0 and either
p + q ≧ 1 or p + q < 0, while the opposite inequality is obtained in case p < 0, q ≧ 1,
p + q < 0, or p > 0, p + q < 0. In all cases, necessary and sufficient conditions are
obtained for equality to hold.
|