A characterization of integral operators on the space of Borel measurable functions bounded with respect to a weight function

Louise Arakelian Raphael

Vol. 26 (1968), No. 2, 361–366

DOI: 10.2140/pjm.1968.26.361

Abstract

Let I be a Borel set of the real line R, C the space of complex numbers, V a σ-algebra of Borel subsets of I, μ a fixed measure on V such that for any bounded set Q ∈ V , μ(Q) < ∞, g(λ,p) a nonvanishing complex valued function μ-measurable in λ ∈ I such that |g(λ,p)|↑ in p where p belongs to a fixed open interval (a,b), and S the set of μ-measurable functions u from I into C such that |u(λ)g(λ,p)|≦ m for some p depending on u,p ∈ (a,b), m ≧ 0 and m depending on u, and for all λ ∈ I. The purpose of this paper is to prove the following:

Theorem 1. Let c(λ,δ) be a μ × μ-measurable function on I × I. For every function u ∈ S the function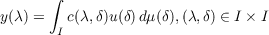

is well defined and y ∈ S if and only if for every p ∈ (a,b) there exists a q ∈ (a,b) such that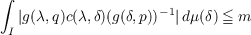

for all (λ,δ) ∈ I × I and some m ≧ 0.

Mathematical Subject Classification

Primary: 47.70

Milestones

Received: 11 August 1967

Published: 1 August 1968