|
|||||

|

|
|

|

|
|
The addition of residue
classes modulo n
Charles Albert Ryavec |
|
Vol. 26 (1968), No. 2, 367–373
|
Abstract |
|
In the present paper, the following is proved: Theorem. Let a1,⋯,am be m distinct, nonzero residues modulo n, where n is any natural number and where 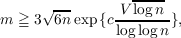 where c > 0 is some large constant. Then the congruence 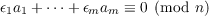 is solvable with 𝜖i = 0 or 1 and not all 𝜖i = 0. The method of proof is completely elementary, in that it is based upon well-known results concerning the addition of residues modulo a natural number n and upon results from elementary number theory. |
Mathematical Subject Classification
Primary: 10.62
|
Milestones
Received: 27 November 1967
Published: 1 August 1968
|
Authors |
| Charles Albert Ryavec | |
 |
