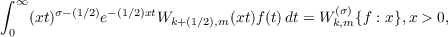Fractional integration and inversion formulae associated with the generalized Whittaker transform

In the present note, we invoke the theories of the Mellin transform as well as fractional integration to investigate a solution of the integral equation

∫ ∞ (xt)σ−(1∕2)e−(1∕2)xtWk+ (1∕2),m(xt)f(t)dt = W (σ){f : x},x > 0, 0 k,m

(*)

which defines a generalized Whittaker transform of the unknown function f ∈ L₂(0,∞) to be determined in terms of its image W_k,m^(σ){f : x}.

It is shown that under certain constraints (*) can be reduced to the form of a Laplace integral which is readily solvable by familiar techniques.

Mathematical Subject Classification

Primary: 44.50

Milestones

Received: 27 November 1967

Published: 1 August 1968

Authors

H. M. (Hari Mohan) Srivastava

Vol. 26, No. 2, 1968

H. M. (Hari Mohan) Srivastava

Abstract

Mathematical Subject Classification

Milestones

Authors