|
Let A be an elliptic convolution
operator of order α on a bounded open set G of Rn, α > 0. Let Aj be the principal part
of A in a local coordinates system and Ãj(xj,ξ) be its symbol with a Wiener-Hopf
type of factorization with respect to ξn : Ãj(xj,ξ) = Ãj+(xj,ξ)Aj−(xj,ξ) for
xnj = 0. Aj+ is analytic in Im ξn > 0, is homogeneous of order k in ξ, k is a
positive integer, k < α. Ãj− is analytic in Im ξn ≦ 0. Let Br;r = 1,⋯,k be a
system of convolution operators on ∂G, of orders αr;0 ≦ αr < α and let
Brj be the principal part of Br in a local coordinates system. The Ãj+,
Brj are assumed to satisfy a Shapiro-Lopatinskii type of condition for each
j.
Visik and Eskin have shown that the operator U from H+s(G) into
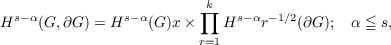
defined by: Uu = {Au,B1u,⋯,Bku} is of Fredholm type. In this paper, we show the
smoothness in the interior of the solutions of Uu = (f,g1,⋅,gk). We prove that if
Ãj+, Brj satisfy a strengthened form of the Shapiro-Lopatinskii condition, then the
operator Uλu = {(A + λα)u,B1u,⋯,Bku} is one-to-one and onto. The nonlinear
problem:
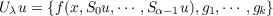
has a solution in H+α(G). f(x,ζ0,⋯,ζα−1) is continuous in all the
variables and has at most a linear growth in (ζ0,⋯,ζα−1). If the set
Ω = {u : u ∈ H+α(G),Bru = 0 on ∂G,r = 1,⋯,k} is dense in L2(G), then the
completeness in L2(G) of the generalized eigenfunctions of the operator A2 associated
with Uu = {f,0,⋯,0} is established.
|