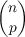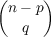|
If f is a function from [0,1] to
the complex plane and c is a complex sequence, then the Hausdorff matrix H(c) for c
and a sequence L(f,c) are defined:
| H(c)np | = 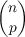 ∑
q=0n−p(−1)q ∑
q=0n−p(−1)q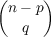 cp+q cp+q | |
| | L(f,c)n | = ∑
p=0nH(c)
npf(p∕n). | | |
This paper consists of the following theorem and two converses to it.
Theorem 1. If A is a complex sequence and ∑
p=0∞Ap is bounded (there is a
number B such that if n is a nonnegative integer then |∑
p=0nAp| < B), f
is a function from [0,1] to the complex plane such that if 0 ≦ x < 1 then
f(x) = ∑
p=0∞Apxp, and c is an absolutely convergent sequence (∑
p=0∞|cp+1 −cp|
converges), then L(f,c) converges. Furthermore, if c has limit d, L(f,c) has limit
∑
p=0∞Ap(cp − d) + f(1)d.
|