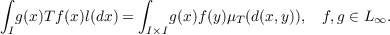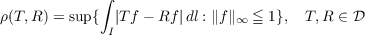|
Let L∞ = L∞[0,1] be the real
Banach space of essentially bounded Lebesgue measurable functions on the unit
interval I = [0,1] with the essential sup-norm. A positive linear operator
T : L∞→ L∞ is called doubly stochastic if (1) T1 = 1, (2) ∫
I Tf dl = ∫
I f dl where l
denotes Lebesgue measure on the unit interval. We denote the set of doubly
stochastic operators by 𝒟. It follows that ∥T∥∞ = 1 for each T ∈𝒟. Let Φ be the
subset of 𝒟 induced by measure preserving maps on the unit interval and Φ1 the
subset of Φ induced by invertible measure preserving maps. For each Tφ ∈ Φ we have
Tφf(x) = f(φ)(x), f ∈ L∞. A regular probability measure μ on the unit square I ×I
is called doubly stochastic if μ(A×I) = μ(I ×A) = l(A) for each A ∈ℬ(I), the Borel
field of the unit interval I. Then there is a one-to-one correspondence between doubly
stochastic operators and doubly stochastic measures. If we denote such a
correspondence by T ↔ μT, then
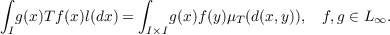
Thus we will identify each T ∈𝒟 with the corresponding doubly stochastic measure
μT ∈ Φ, the doubly stochastic measure μφ = μTφ is singular with respect
to Lebesgue measure l2 on the unit square. Let L be the set of all T ∈𝒟
such that μT is absolutely continuous with respect to l2, i.e., μT ≪ l2. The
metric
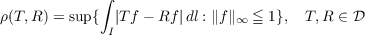
defines a topology on 𝒟 which will be called the uniform topology. The purpose of
this paper is to show that each T ∈ L can be approximated by a convex combination
of operators from Φ in the uniform topology, called the uniform approximation
theorem.
|