Integral inequalities involving second order derivatives

James Calvert

Vol. 27 (1968), No. 1, 39–47

DOI: 10.2140/pjm.1968.27.39

Abstract

An integral inequality involving second order derivatives is derived. A most important consequence of this inequality is that the Dirichlet form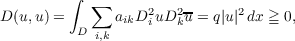

for functions q(x) which are positive and “not too large” in a sense which will be made precise later and for functions u(x) with compact support contained in D. Some examples are given and an application is made to an existence theorem for a fourth order uniformly elliptic P.D.E.

Mathematical Subject Classification

Primary: 35.19

Milestones

Received: 8 June 1967

Published: 1 October 1968