|
Let A be a finite-dimensional
associative algebra with identity over a field k, M an A-module which is
finite-dimentional as a vector space over k, and E = Homk(M,M) the algebra of
linear transformations on M. For a ∈ A. Let aL denote the linear transformation of
M given by aL(x) = ax, for x ∈ M. Define the following subalgebras of
E:
| AL | = {aL : a ∈ A} | |
| | C | = {f ∈ E : f(ax) = af(x) for each a ∈ A,x ∈ M} | |
| | D | = {f ∈ E : f(g(x)) = g(f(x)) for each g ∈ C,x ∈ M}. | | |
Clearly, AL ⊆ D. Require M to be faithful. Then A is isomorphic to, and will be
identified with, AL. If A = D, it is said that the pair (A,M) has the double
centralizer property.
A is called a QF-1 algebra if (A,M) has the double centralizer property for each
faithful A-module M.
The following results in the theory of QF-1 algebras are obtained:
1. Let A be a commutative algebra over an arbitrary field. Then A is QF-1 if and
only if A is Frobenius.
2. Let A be an algebra such that the simple left A-modules are one-dimensional.
Suppose there exist distinct simple two-sided ideals A1 and A2 contained in the
radical of A, and primitive idempotents e and f, such that eAkf≠0, for k = 1,2.
Then A is not QF-1.
3. Let A be an algebra with the properties that the simple left A-modules are
one-dimensional, and the two-sided ideal lattice of A is distributive. Then if A
satisfies any one of the following conditions, it is not QF-1.
(a) There exist, for r ≧ 2, 2r distinct simple two-sided ideals Auv contained in the
radical, and primitive idempotents eiu and ejv for 1 ≦ u, v ≦ r, satisfying
eiuAuvEjv≠0, where the index pair (u,v) ranges over the set
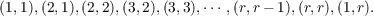
(b) There exist, for r ≧ 1, 2r + 2 distinct simple two-sided ideals Auv and Avρ, for
(u,v) = (1,1),(1,2),⋯,(r − 1,r − 1),(r − 1,r), and (ρ,v) = (1,1),(2,1),(3,r), and
(4,r), and primitive idempotents eiu, ejv, and ekρ satisfying eiuAuvej≠0 and
ekρAvρejv≠0, where (u,v) and (ρ,v) range over the index pairs indicated
above.
|