|
The interchange graph I(G) for
an unoriented graph G has been defined by Ore as follows: The vertices of I(G) are
the edges of G; and two vertices of I(G) are connected by an edge if and only if they
are adjacent (i.e., have a vertex in common) in G. In 1962 Ore raised the problem of
determining those graphs for which
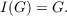 | (1) |
This paper solves this problem for finite connected graphs with loops and parallel
edges, extending earlier work on the problem.
A loop (an edge whose two ends coincide in a single vertex) is considered adjacent
to itself, and hence generates another loop under the I mapping. If two edges of G
connect the same two vertices, the corresponding vertices of I(G) are also connected
by two distinct edges.
|